The Algorithm

In order to implement this process in the computer, there are some things you must remember.

1. When doing floating point arithmetic, the computer will introduce round-off errors that will interfere with finding the correct answer. To avoid this, we must represent our numbers in a format that can be represented exactly.
2. Because we are working in modulo 2 arithmetic, we have to make sure we keep our numbers in the range 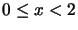. Ultimately, we want our final answers to be integers as well, so you need to keep that in mind, too.
3. Because some boards will not have a valid solution, we have to test our solutions. Boards without winnable solutions will generate answers; they just won't work.

To facilitate number 1, I have created a fraction datatype which consists of two integers, a numerator and a denominator. There are functions for performing basic operations on these fractions, including multiplication, division, addition, subtraction, and reciprocals. Also, the fractions are automatically reduced after each operation (this is necessary to keep the integers from overflowing).

The first step in generating a solution is to create the matrix. The matrix_new function creates a 26x25 matrix as shown above, with the final column representing the board position we are attempting to reach. The elements in this matrix use the fraction datatype. Once created, we are ready to call the function gauss to do the Gauss elimination.

After reducing each row in the matrix, I multiply each element in the row by the least common multiple (LCM) of the row's denominators. This has the effect of converting the row to all integers. Then I perform the modulo 2 arithmetic to force everything to either a 0 or 1.

After the Gauss elimination is complete, the find_solutions function fills in the two free variables with all four combinations of 0's and 1's to generate four solutions. It keeps only the simplest of the four, and returns that as the answer.