Next: The Algorithm Up: XLightOff Solver Previous: XLightOff Solver

The Solution

In this document, I will attempt to explain how my solver works. But before I begin, there are a few properties of the game which must be understood.

You should never have to press a button more than once to solve any puzzle.
The order in which the buttons are pressed is irrelevant.
The same buttons which will turn all the lights off will, if started from a blank board, get you back to the original puzzle (this one makes the math a little easier).

Given these rules, we can begin by looking at each button individually. For the rest of this document, we will assume we are starting from a blank board and trying to recover the puzzle. Suppose we number the buttons as follows.

$b_{0}$	$b_{1}$	$b_{2}$	$b_{3}$	$b_{4}$
$b_{5}$	$b_{6}$	$b_{7}$	$b_{8}$	$b_{9}$
$b_{10}$	$b_{11}$	$b_{12}$	$b_{13}$	$b_{14}$
$b_{15}$	$b_{16}$	$b_{17}$	$b_{18}$	$b_{19}$
$b_{20}$	$b_{21}$	$b_{22}$	$b_{23}$	$b_{24}$

Let's look at the top left button, $b_{0}$ . The state of this light is determined by how many times we push it and its neighbors, $b_{1}$ and $b_{5}$ . If the total number of presses of these three buttons is even, the light will be off. If it's odd, the light will be on. Now let's look at $b_{12}$ , right in the middle of the board. The same applies here, except that there are 5 buttons which will determine its final state: $b_{7}$ , $b_{11}$ , $b_{12}$ , $b_{13}$ , and $b_{17}$ .

To express this mathematically, we could say

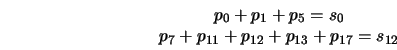
$\begin{displaymath} \begin{array}{c} p_{0}+p_{1}+p_{5}=s_{0}\\ p_{7}+p_{11}+p_{12}+p_{13}+p_{17}=s_{12} \end{array}\end{displaymath}$

Where $p_{n}$ represents the number of times we press button $b_{n}$ , and $s_{n}$ is the state of the light afterwards. We can write equations like this for all 25 buttons, which would give us a system of 25 linear equations with 25 variables. If we solve this system for a given set of states $\left( s_{0..24}\right)$ , we will have a solution to the puzzle.

To facilitate solving these equations, we will rewrite the system as a matrix and use Gauss elimination to solve the puzzle. The matrix looks like this.

$\begin{displaymath} \left[ \begin{array}{ccccccccccccccccccccccccc} 1 & 1 & 0 & ... ...20}\\ s_{21}\\ s_{22}\\ s_{23}\\ s_{24} \end{array}\right] \end{displaymath}$

The rest of the work involves setting the values for $s_{0..24}$ (0's and 1's) and solving the matrix using modulo 2 arithmetic. If you perform Gauss elimination on this matrix, you will find that you end up with two free variables, $p_{23}$ and $p_{24}$ . What this means is that there are four solutions, and if you want to find the shortest one, you will need to try them all. It should also be noted that not all boards have a workable solution, so you will need to test for that also.

Next: The Algorithm Up: XLightOff Solver Previous: XLightOff Solver

James Williams 2002-01-12